25 ++ 鋭角三角形 条件 296172-鋭角三角形 条件 証明
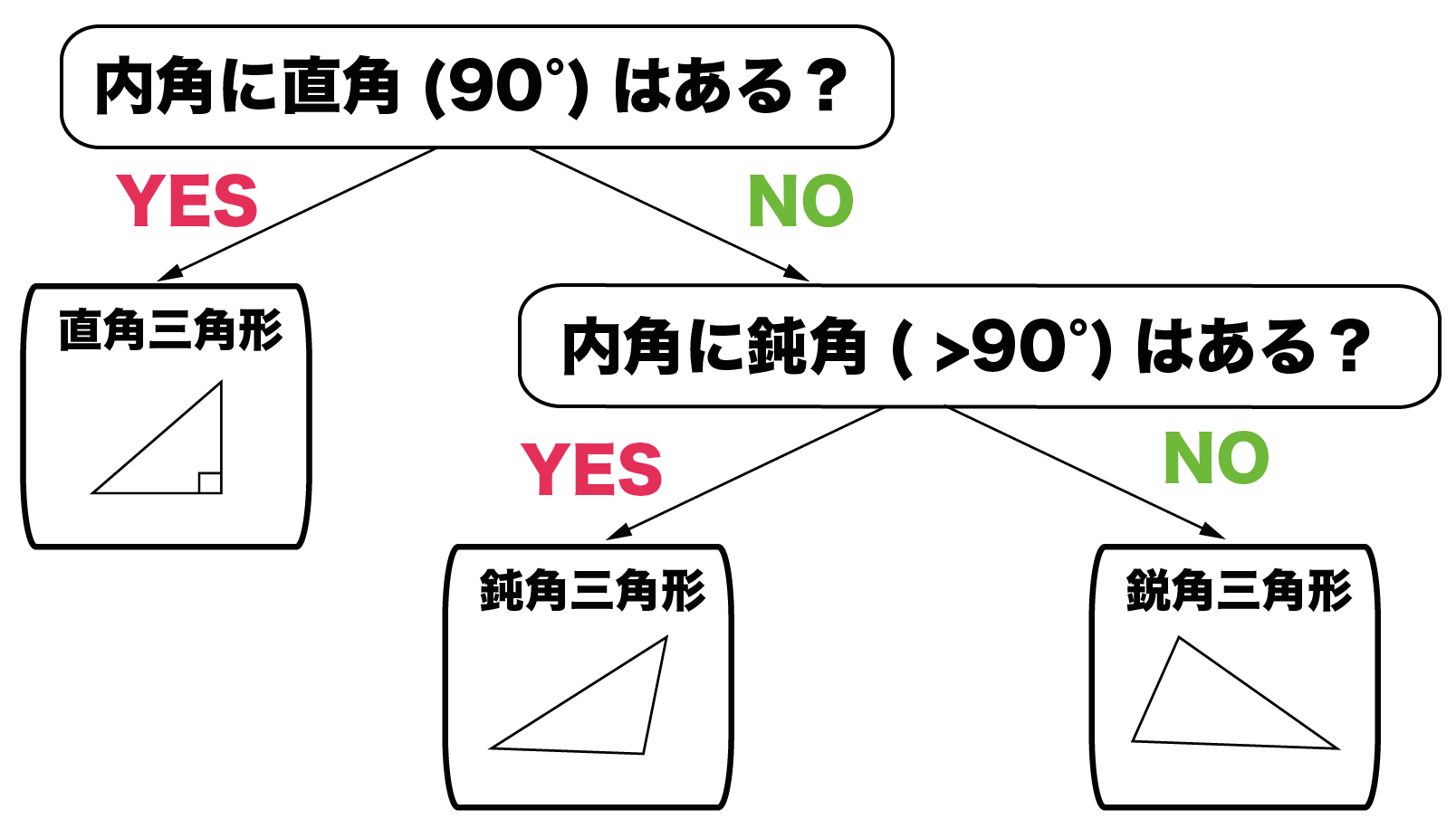
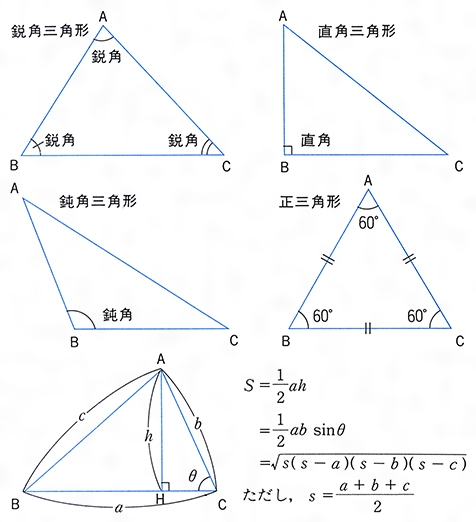
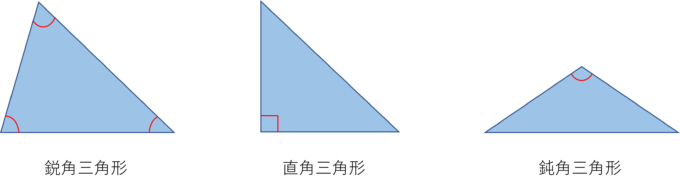
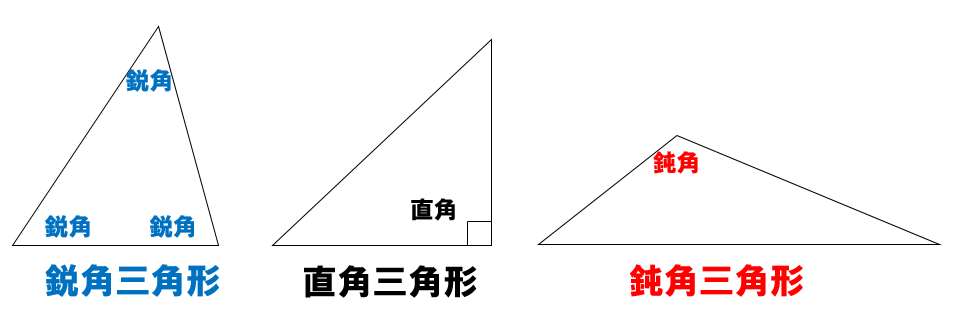
三角形種類
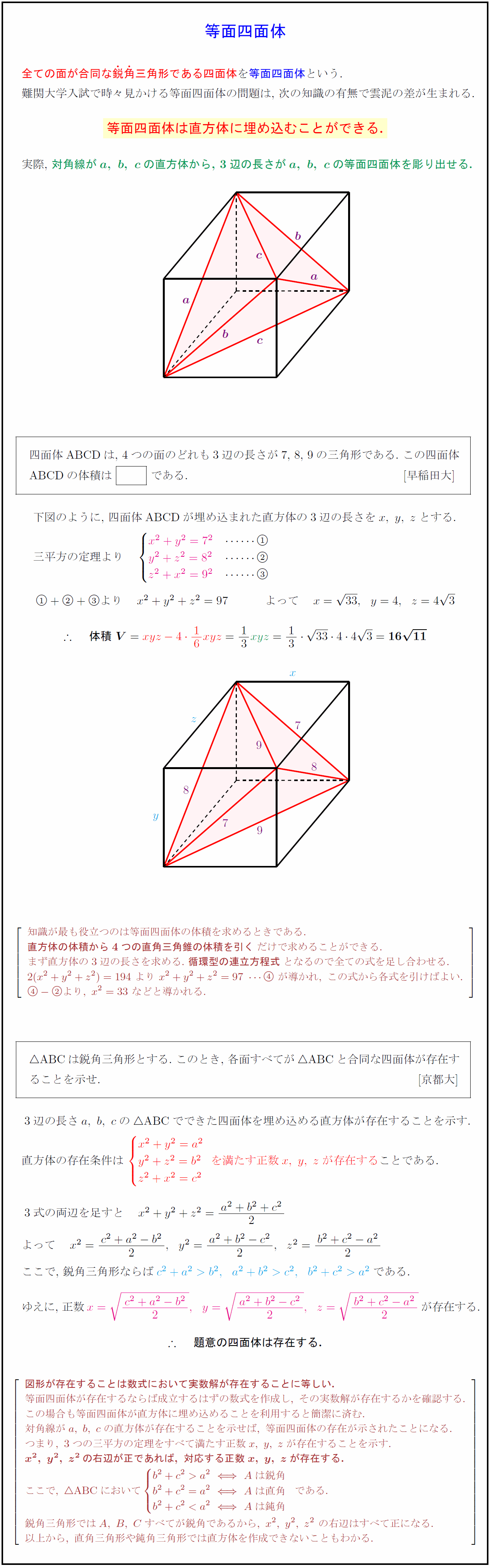
問題① 3つの内角のうち、2つが60°,45°である三角形は、 鋭角三角形、直角三角形、鈍角三角形のどれでしょう? 三角形の3つの内角のうち2つがわかっているので、残りの1つの角ゆえに、鋭角三角形と鈍角三角形の出来る確率は等しい。 逆は必ずしも真ならずですが、今度はこれでいいような気がします。 如何なものでしょうか。 ところで、直角三角形は、鋭角三角形と鈍角
鋭角三角形 条件 証明
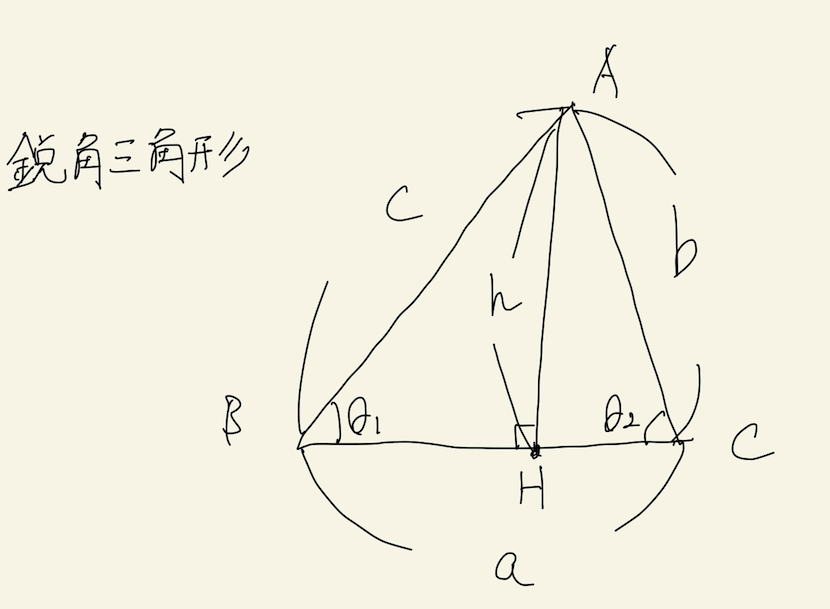
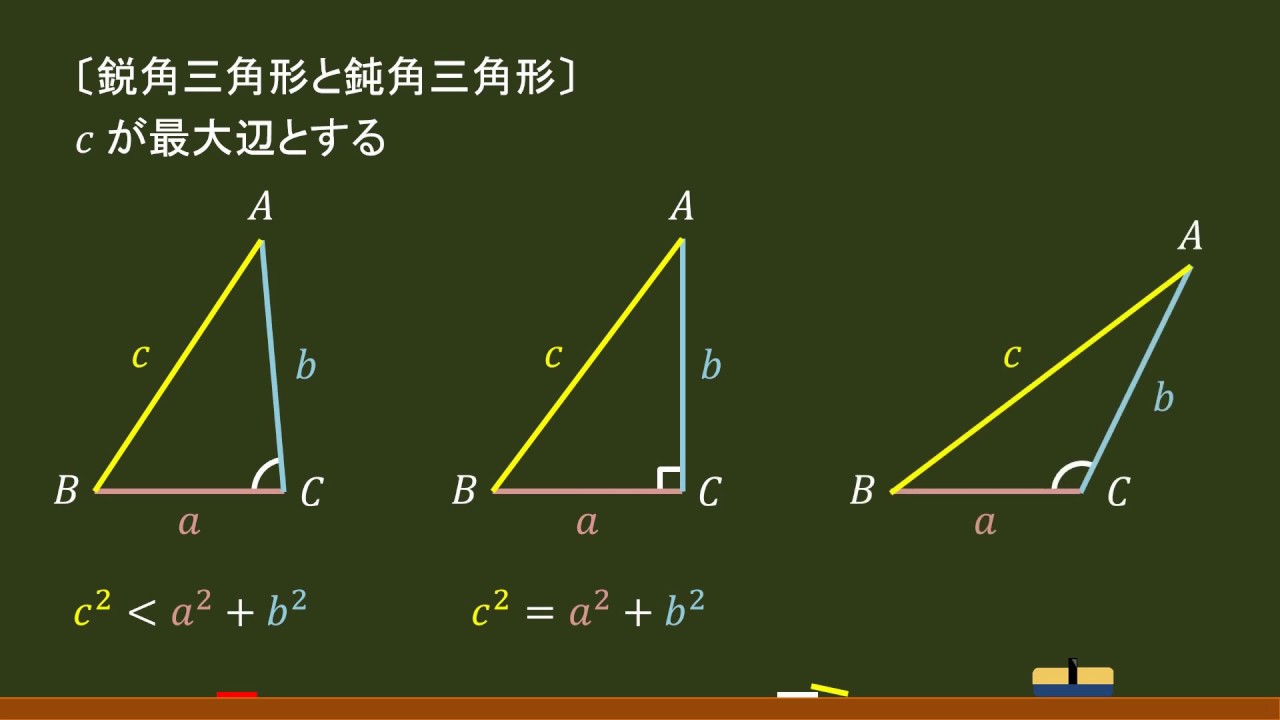
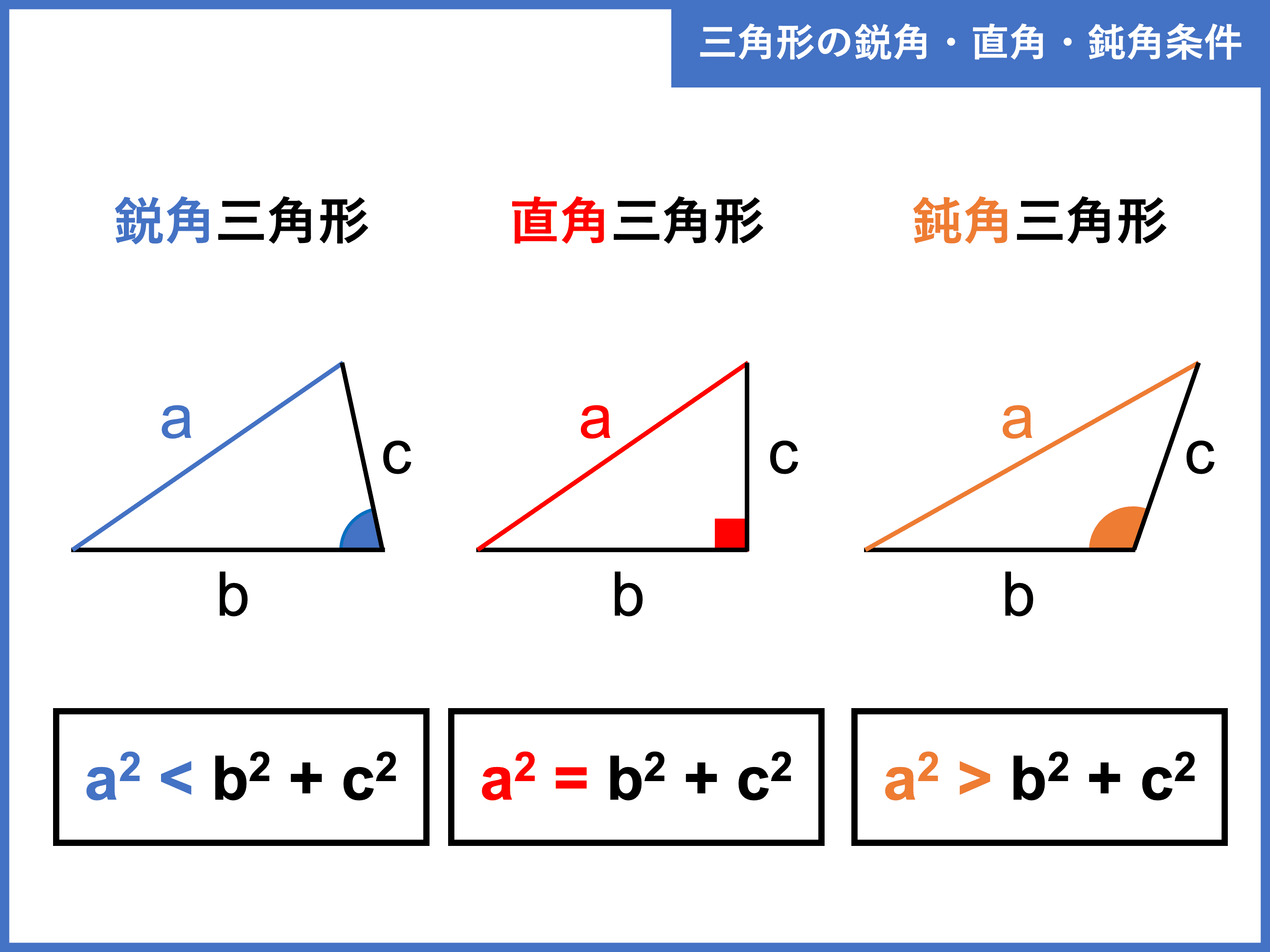
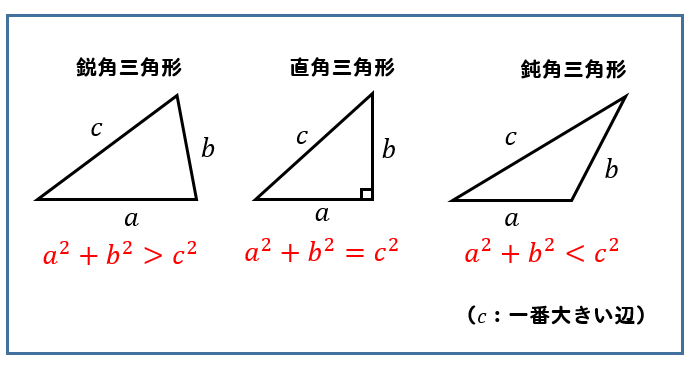
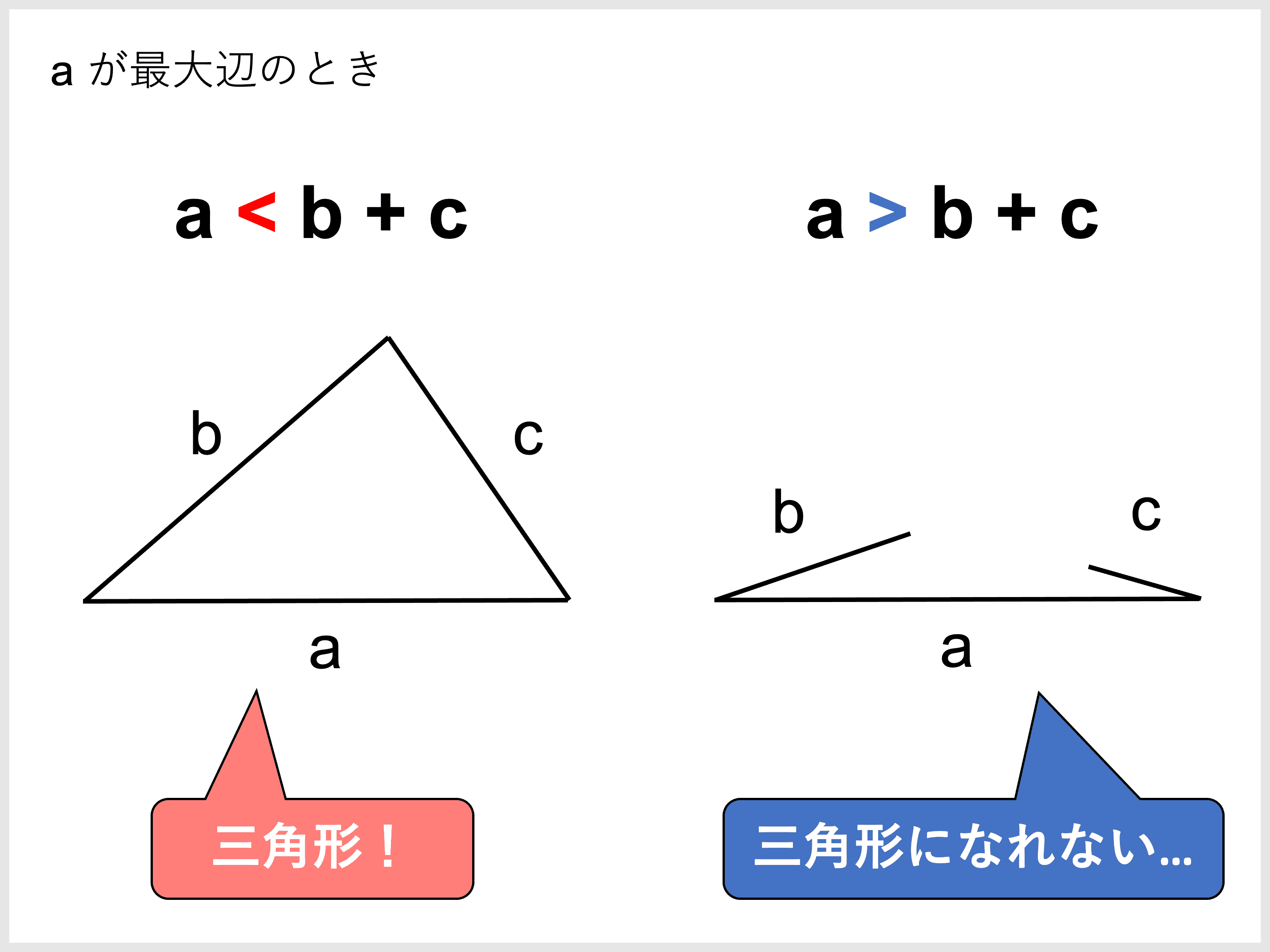
鋭角三角形 条件 証明-るので,三角形の成立条件は a < bc となる.直角三角形,鋭角三角形,鈍角三角形のいずれであるかを調べるときに 三角形の成立条件を前提としなければならないのか? 実は,直角三角形,鋭角 鋭角三角形になる条件 a^2 < b^2 c^2 と直角三角形になる条件 a^2 = b^2 c^2 は、おのずと三角形の成立条件 a < b c を満たします。 一方、鈍角三角形になる条件 a^2 > b^2 c^2
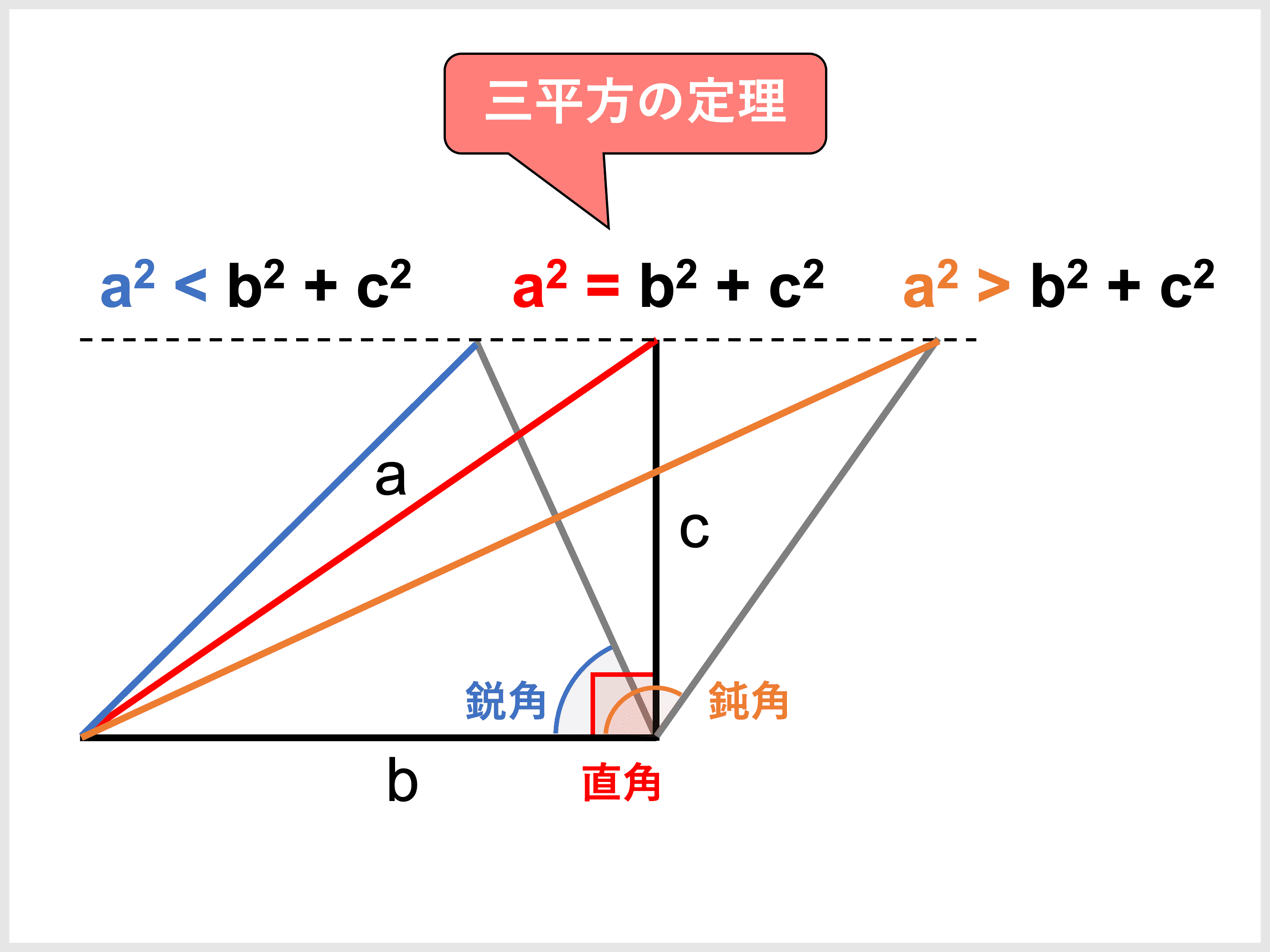
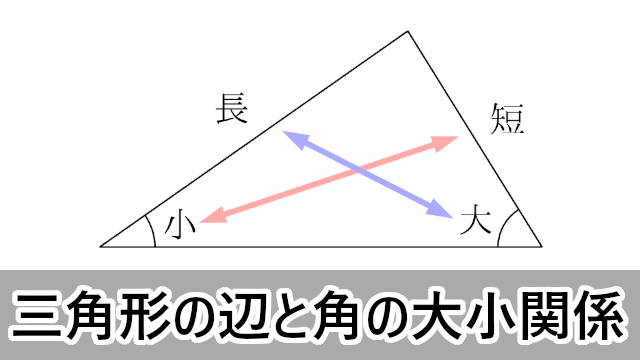
三角形の成立条件 辺と角の大小関係をわかりやすく解説 受験辞典
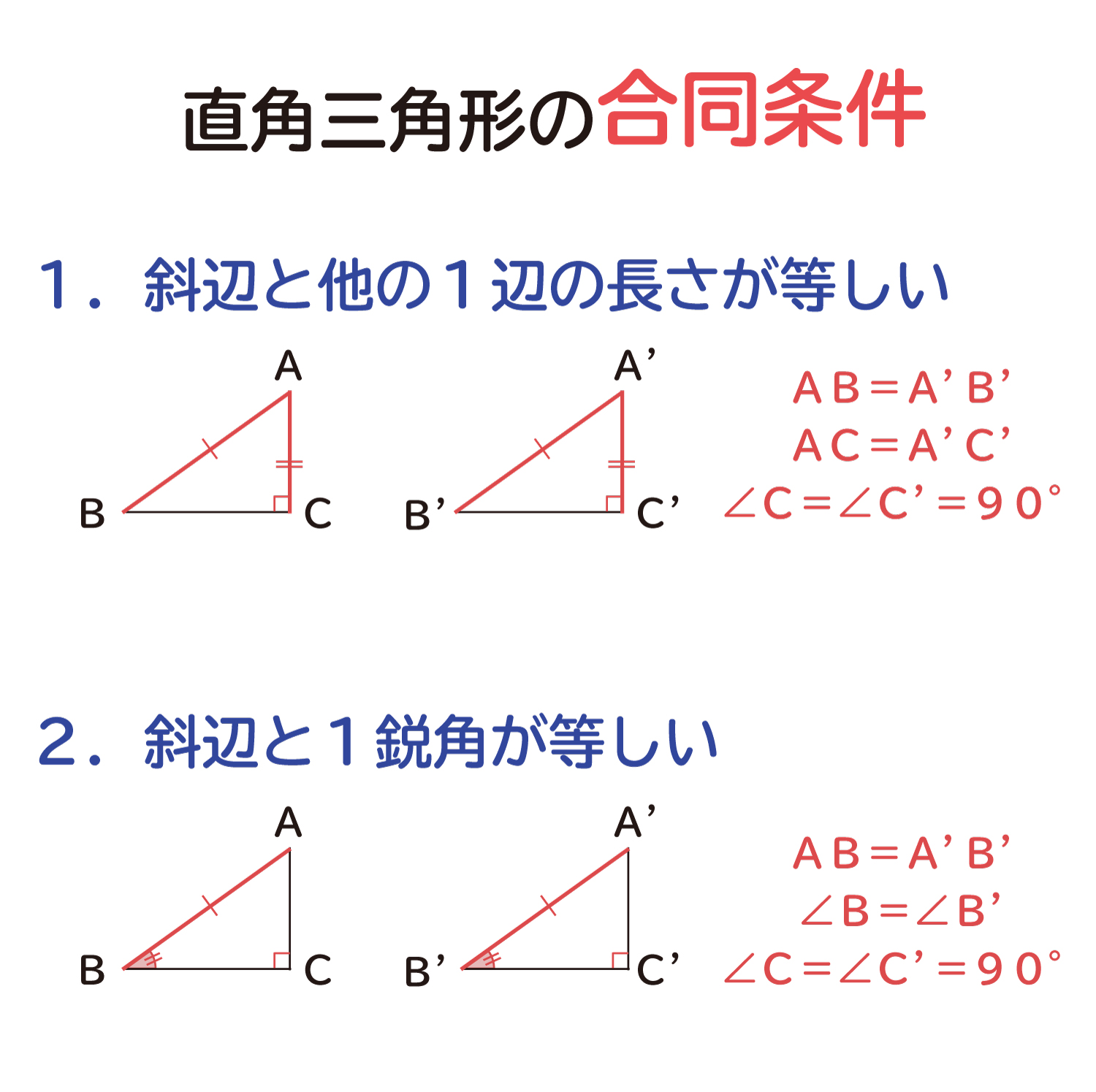
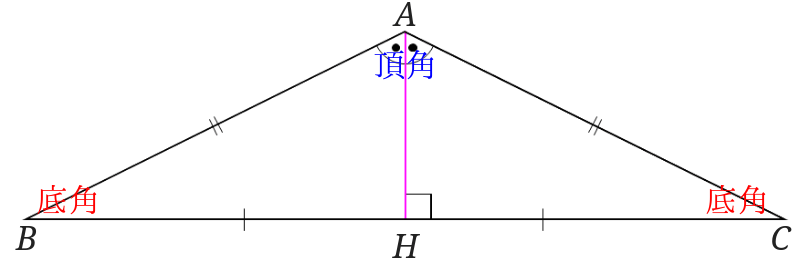
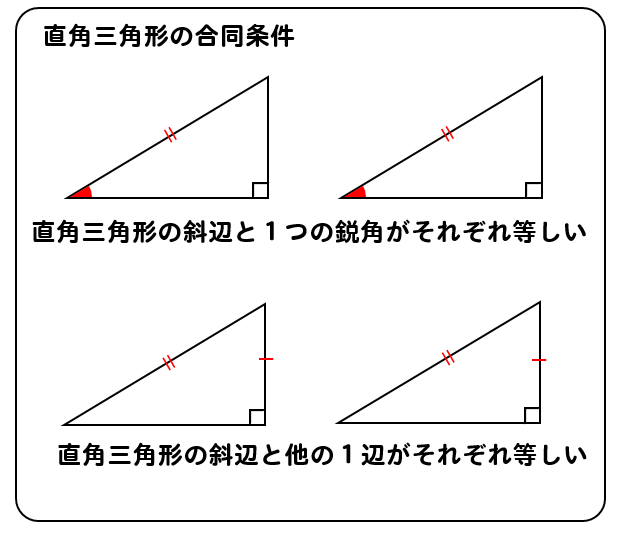
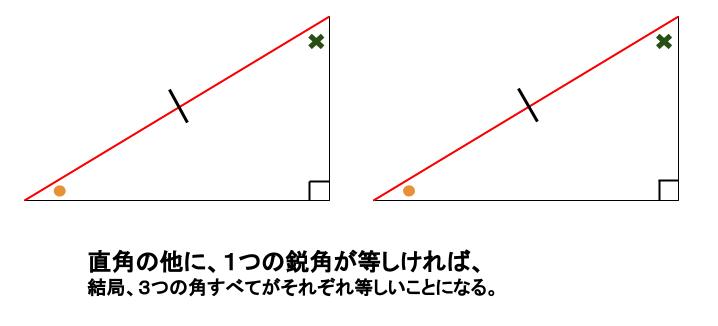
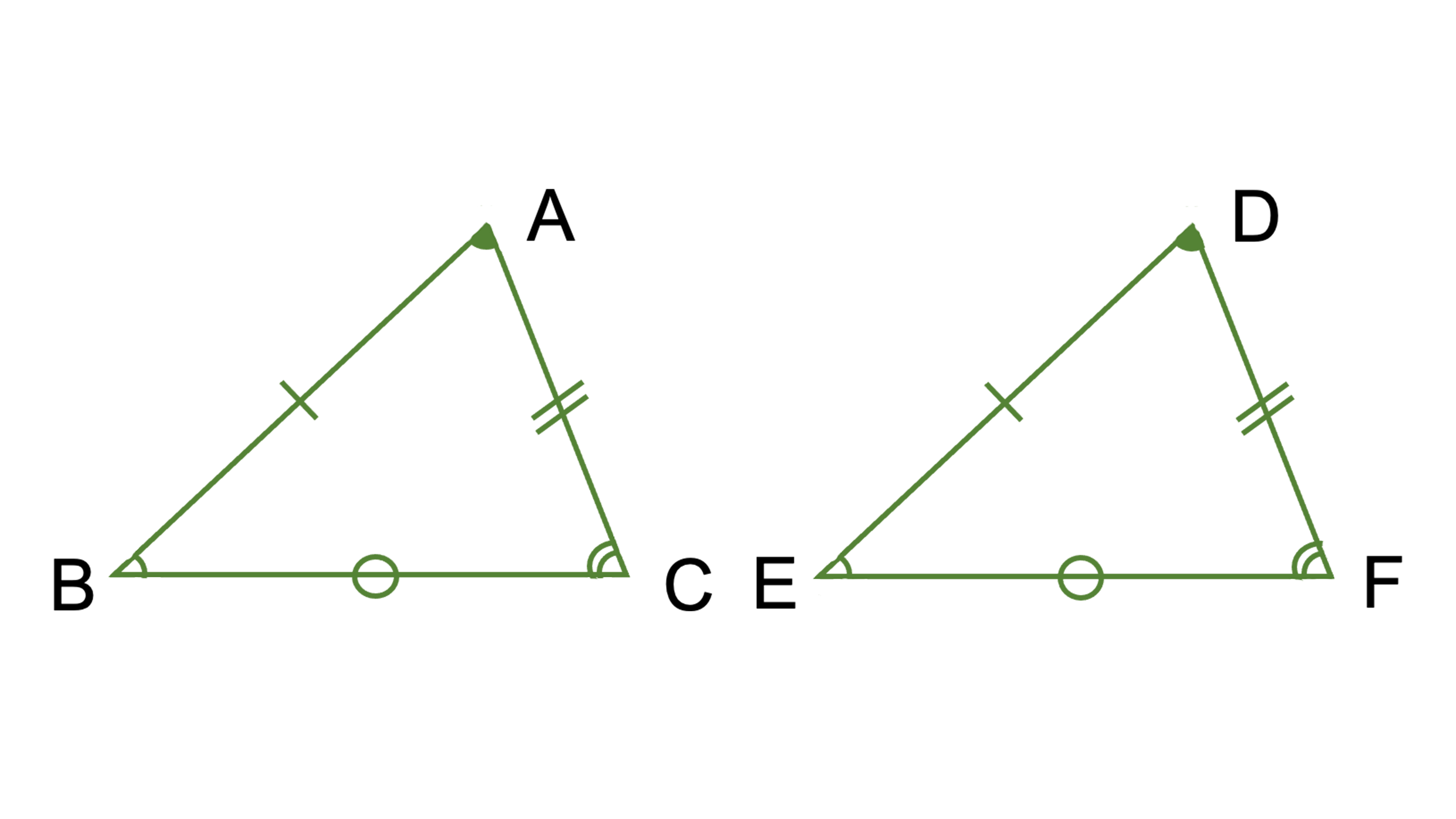
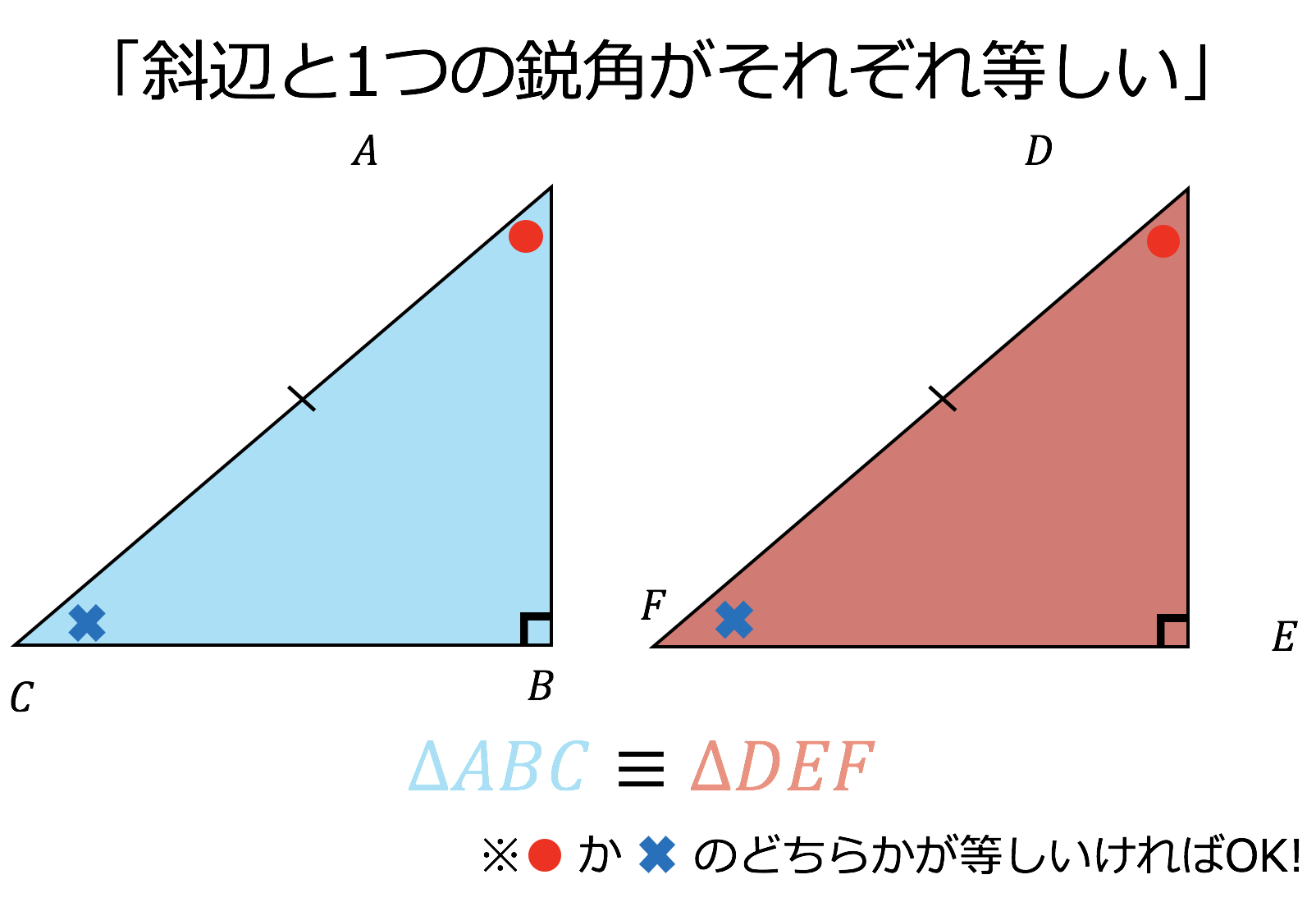
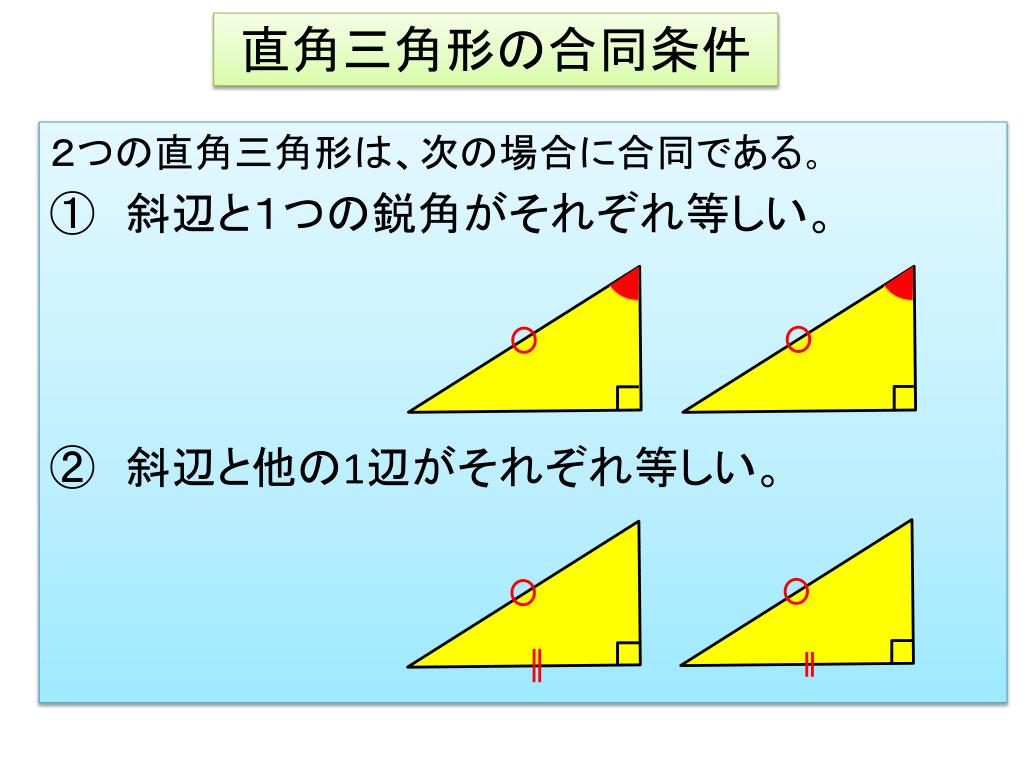
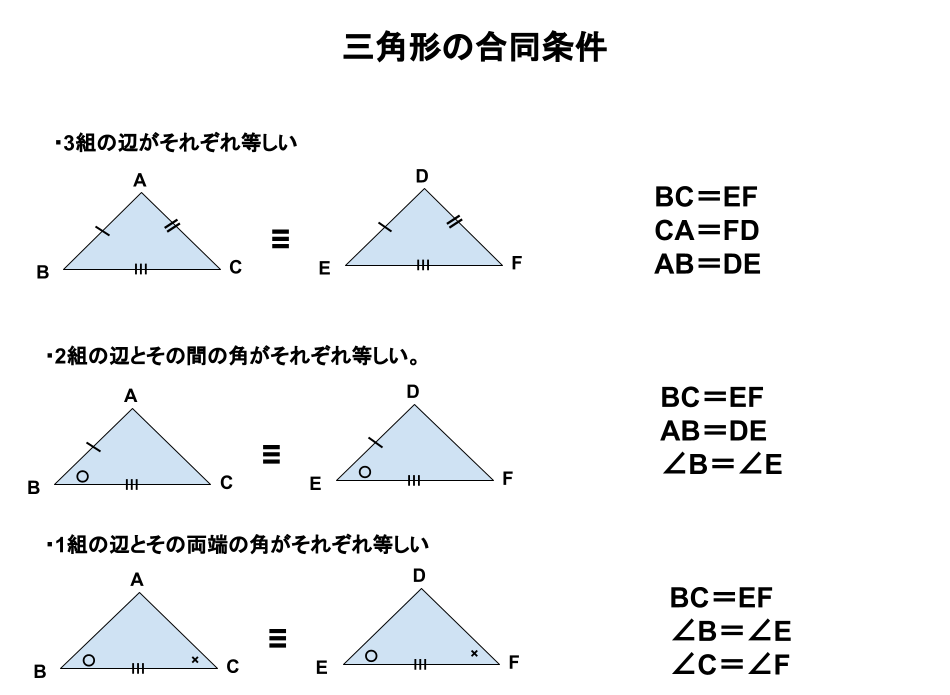
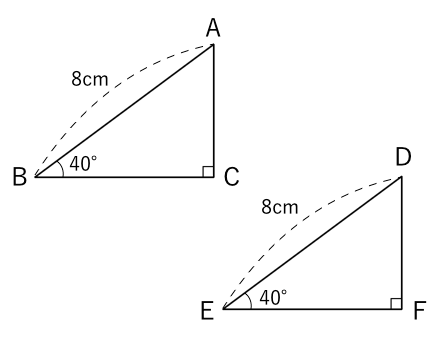
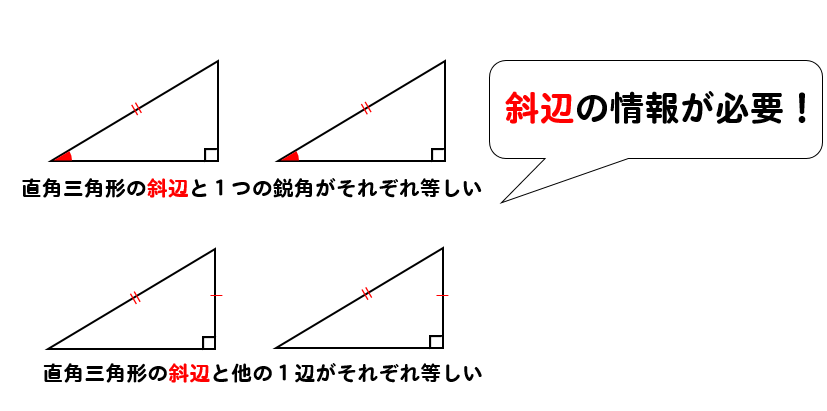
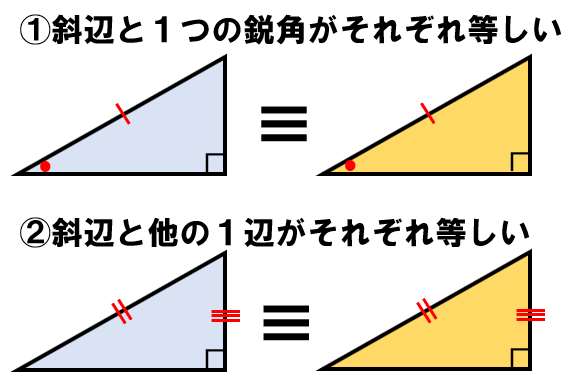
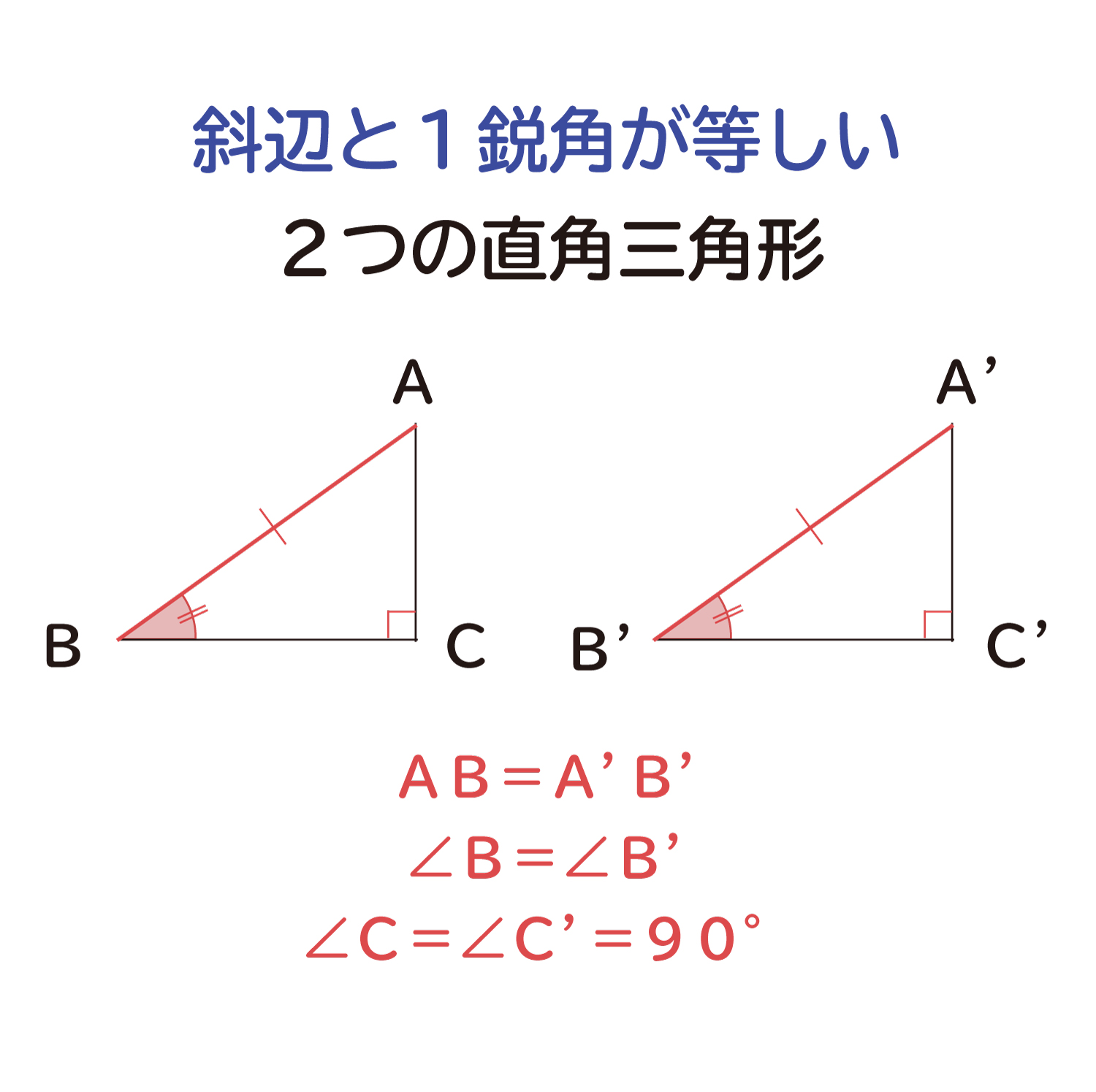
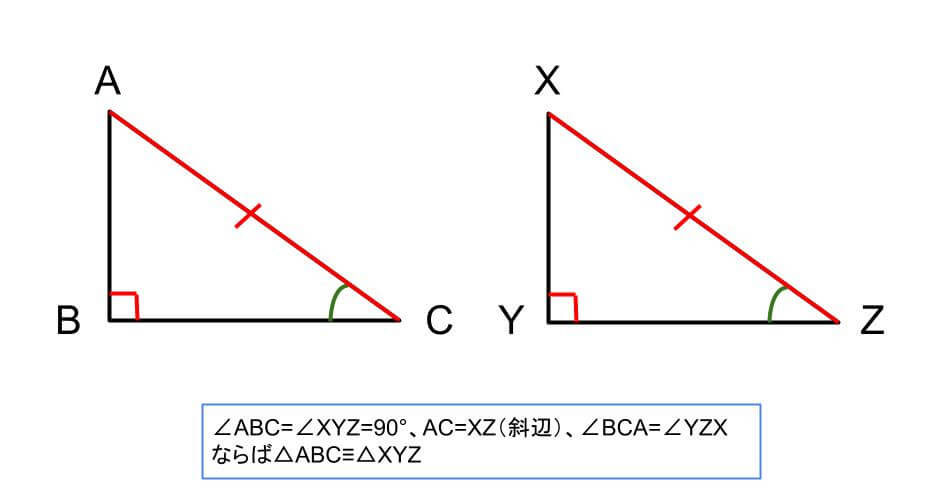
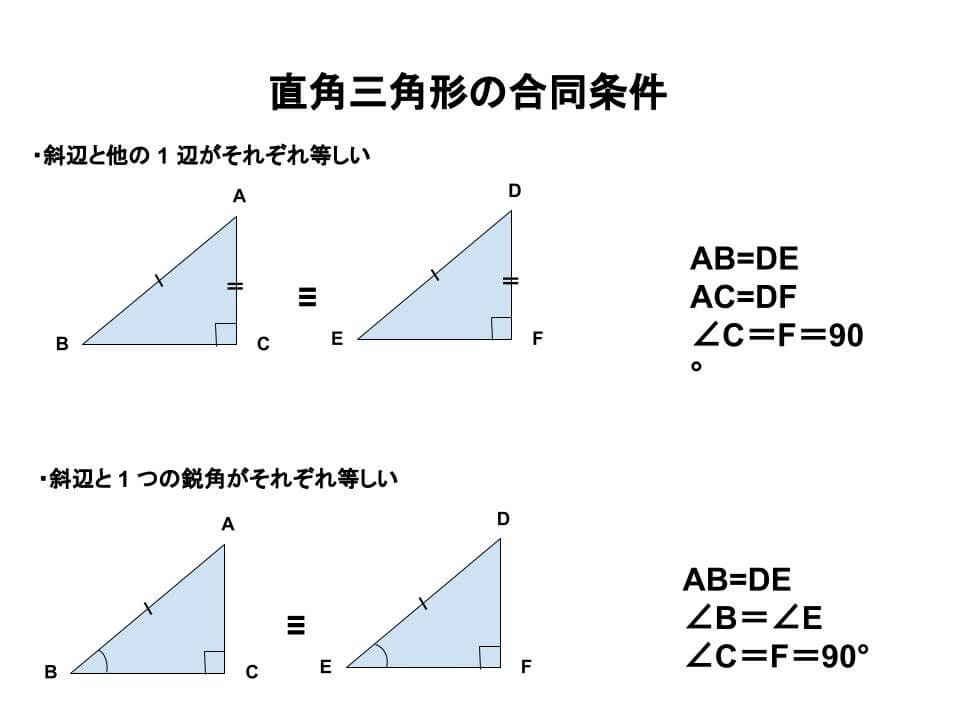
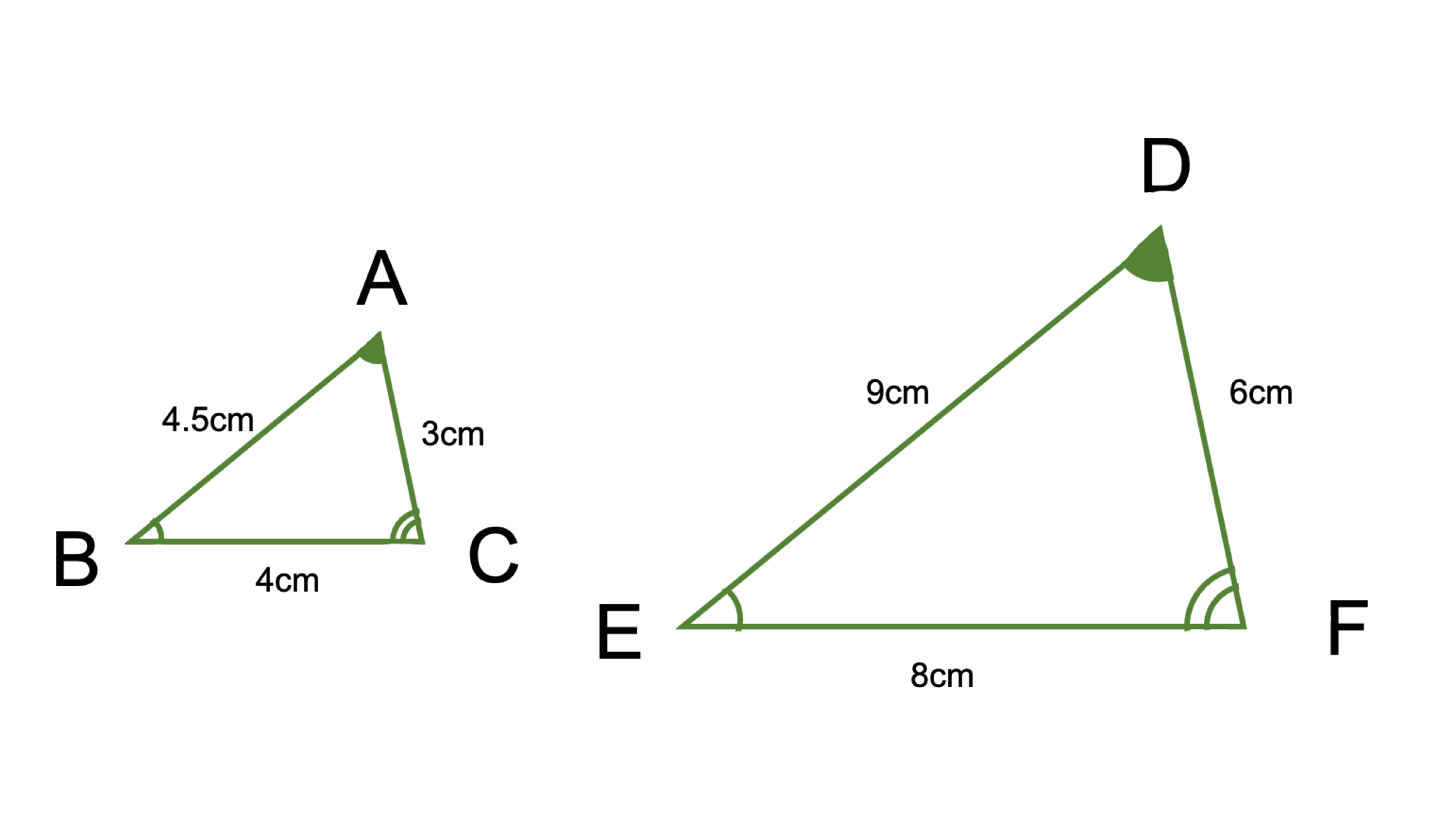
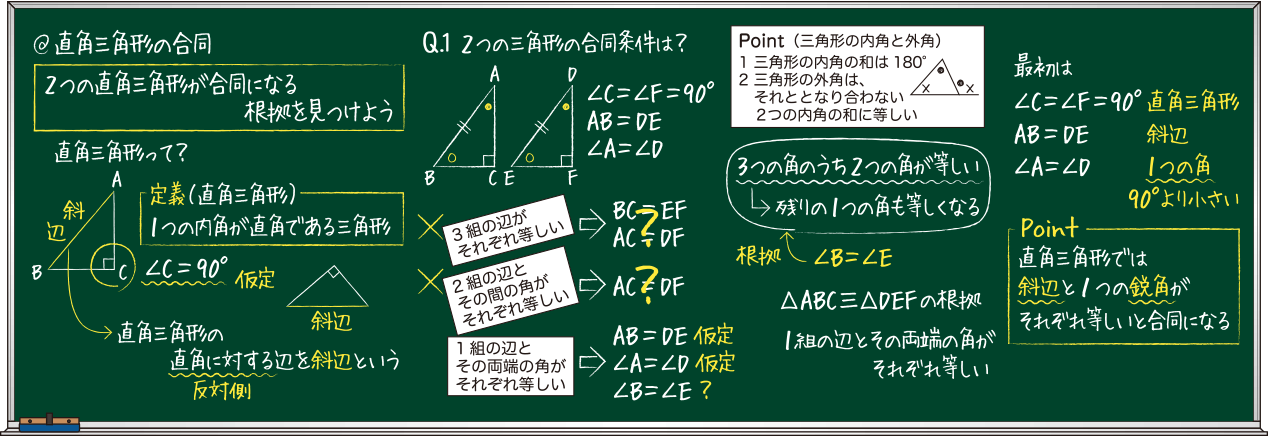
三角形の合同条件は全部で5つです。 三角形の合同条件に加えて、直角三角形の合同条件を覚えるようにしましょう。 ・斜辺と1つの鋭角がそれぞれ等しい なお、日本では直角三角形の合同条件とし鋭角三角形になるための条件 19年1月7日 mantora コメントをどうぞ 中心Bの円の半径を3、Aは円の円周を A1からA5 A 1 か ら A 5 まで移動する ものとし、 BC=5とする。 ∠CはAB=3で最大辺で直角三角形の合同条件に出てくる 「鋭角」 というのは、 90°より小さな角 のことだよ。 ここでは、簡単に言うと 「直角でない2つの角のうちの1つ」 を指すよ。 ちなみに、 90°よりも大きな角 の
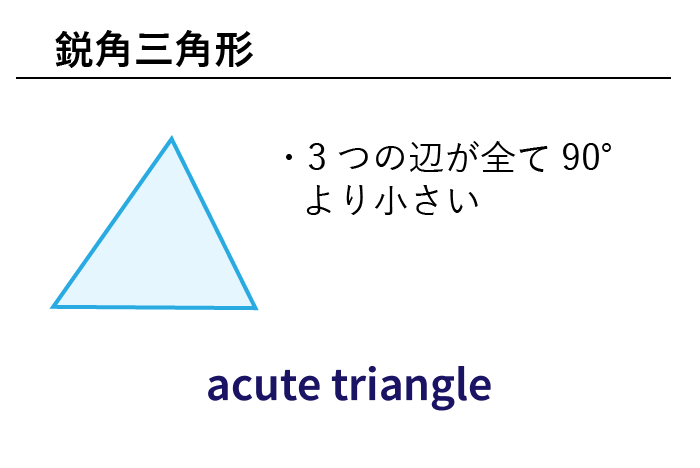
鋭角三角形 (えいかくさんかっけい、 英 acute‐angled triangle )は、 三角形 の一種で、すべての角が 直角 (90 ° =π/2 rad) よりも小さい 図形 である。 なお、鋭角三角形では、長辺をc、短辺をa,b三平方の定理とは 直角三角形のときに利用できる 辺の長さの関係式でしたね。 それを発展させて考えていくと 直角三角形だけでなく 鋭角、鈍角三角形を見分ける方法として活用することができ直角三角形の合同条件 2つの直角三角形は、次の場合に合同である。 1 斜辺と1つの鋭角が、それぞれ等しいとき(証明) 2 斜辺と他の1辺が、それぞれ等しいとき(証明)証明)
鋭角三角形 条件 証明のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | 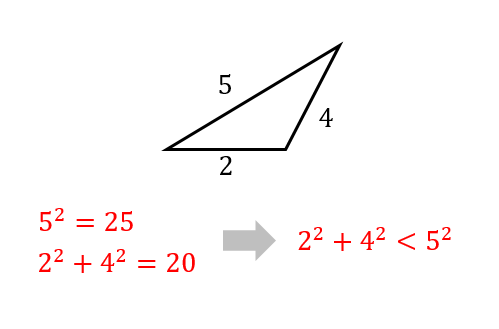 |  |
 |  | |
 |  | |
「鋭角三角形 条件 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「鋭角三角形 条件 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「鋭角三角形 条件 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 1-1problem.png) | |
 | ||
 | ||
「鋭角三角形 条件 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「鋭角三角形 条件 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「鋭角三角形 条件 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「鋭角三角形 条件 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「鋭角三角形 条件 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「鋭角三角形 条件 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
「鋭角三角形 条件 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「鋭角三角形 条件 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
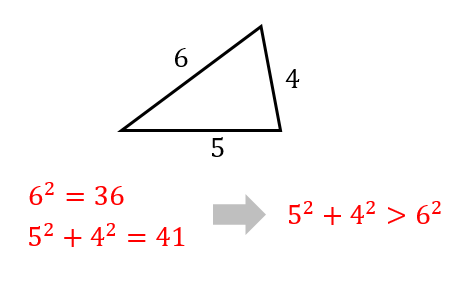 |
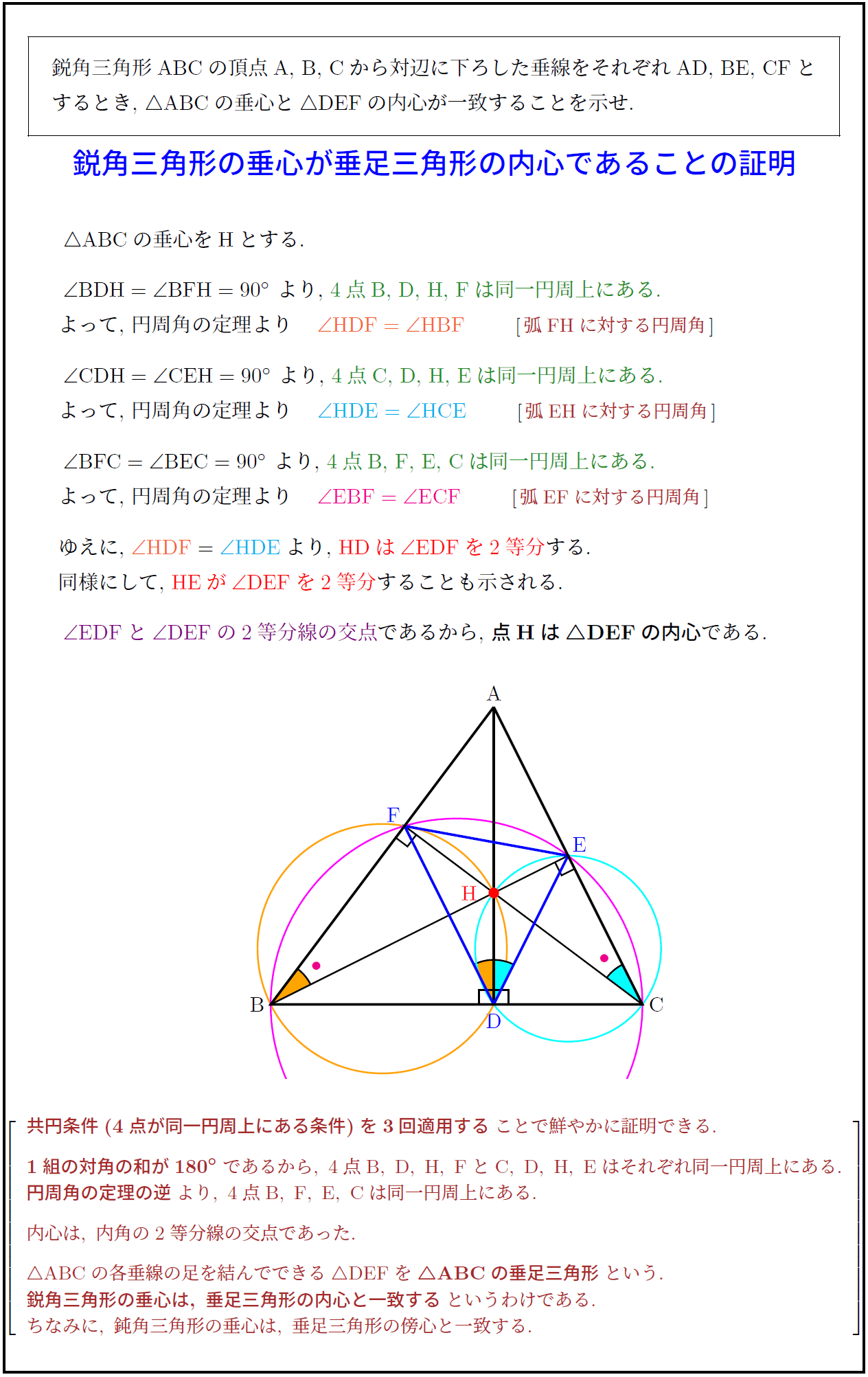
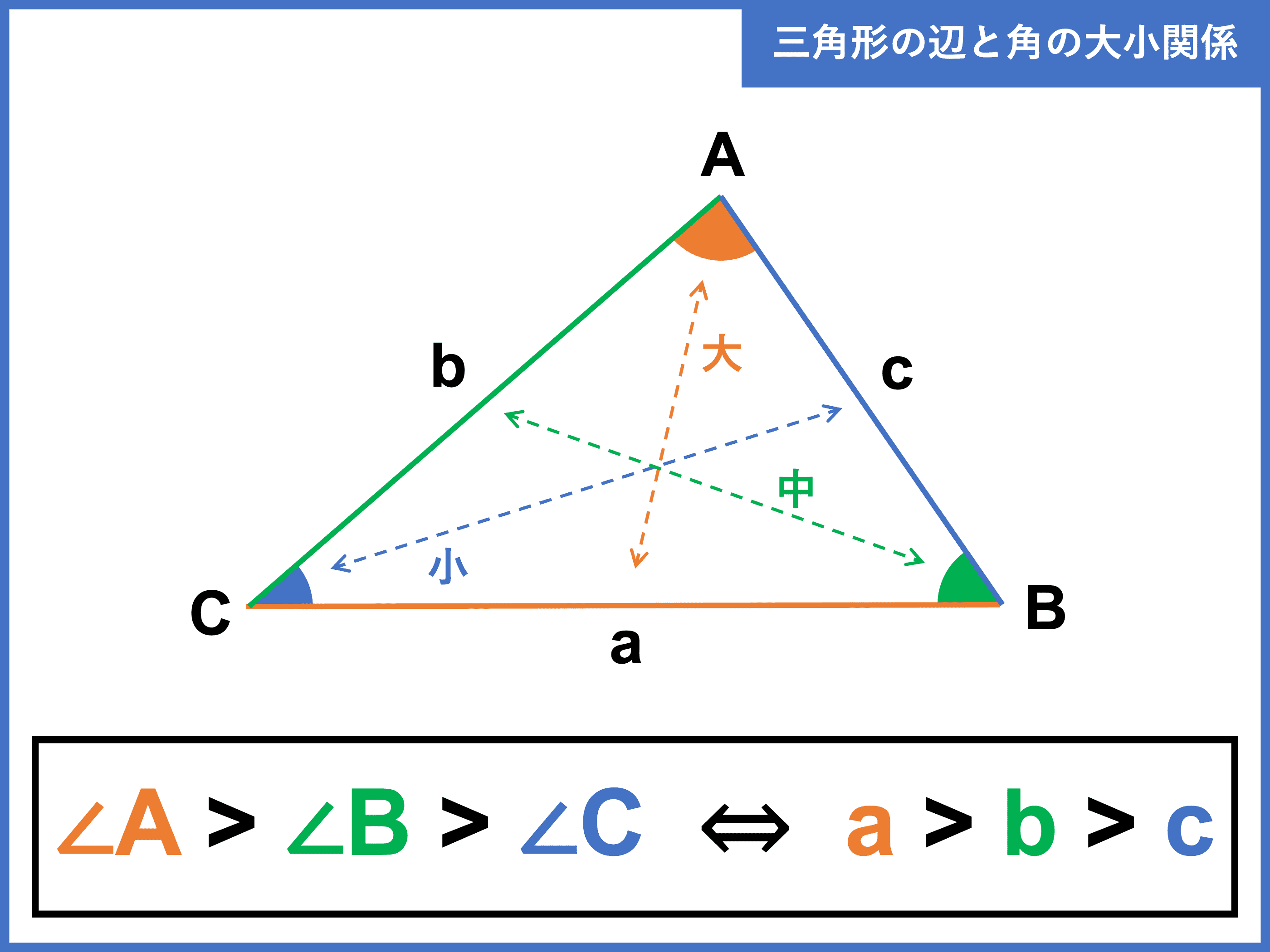
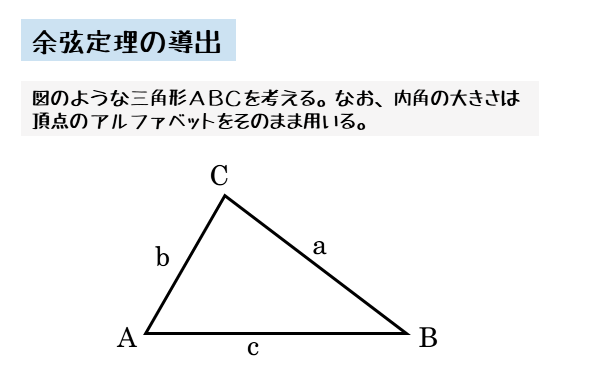
辺と角の大小 三角形の辺同士や角同士の大小関係を意識すると,議論が簡単になる場合があります。 例えばある三角形が鋭角三角形であることを証明するには,最大角が鋭角であることを示せば こいつは「 鋭角 」だ。 (2)角Cについて Cをクローズアップしてみると、 40° であることがわかる。 こいつはどっからどうみても90°より小さいから、 「 鋭角 」だね。 (3)角Aについ
Incoming Term: 鋭角三角形 条件, 鋭角三角形 条件 辺の長さ, 鋭角三角形 条件 ベクトル, 鋭角三角形 条件 中学, 鋭角三角形 条件 証明, 鋭角三角形 条件 複素数, 鋭角三角形 条件 角, 鋭角三角形 条件 長さ, 鋭角三角形 条件 範囲, 鈍角三角形 鋭角三角形 条件,
コメント
コメントを投稿